Enumeration of Deltahedral Graphs with up to 10 Vertices
Abstract
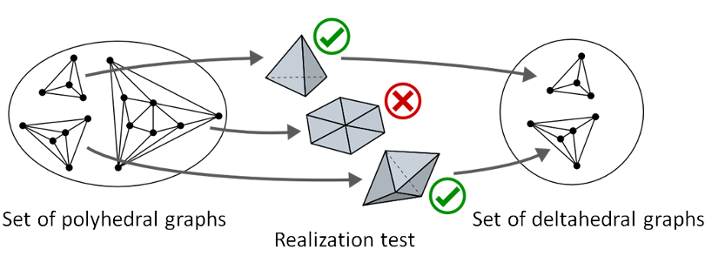
In this paper, we enumerate the polyhedral graphs that are realizable as deltahedra with up to ten vertices. We call these "deltahedral graphs". This result was achieved by an experimental approach that trying to construct deltahedra from each of the simple cubic polyhedral graphs. We also provide examples of the graphs that are not realizable as deltahedra. We show that the infinite families of such nonrealizable graphs can be obtained by solving the graph isomorphism problem.
概要
本研究では,頂点数10までの多面体グラフのうちデルタ多面体として実現可能なものを数え上げる.そのようなグラフを"デルタ多面体グラフ"と呼ぶ.数え上げの結果は,すべての3次多面体グラフからデルタ多面体の再構築を試みるという実験的な手法により得られた.この結果より,3次多面体グラフにはデルタ多面体として構築できないグラフが含まれることが確認された.さらに本稿では,部分グラフ同型問題を解くことで,構築不可能なグラフのセットを得る手法も提案する.
Supplemental Material
List of reconstructed polyhedra.
Publication
- Naoya Tsuruta, Jun Mitani, Yoshihiro Kanamori and Yukio Fukui, "Enumeration of Deltahedral Graphs with up to 10 Vertices", The 16th International Conference on Geometry and Graphics (ICGG2014), Innsbruck, Austria, August 4–8, 2014. PDF
- 鶴田直也, 三谷純, 金森由博,福井幸男, "面数が16以下の非凸デルタ多面体の数え上げ", 2012年度 日本図学会秋季大会, 東京, 学術講演論文集, pp.63-68, 2012/12/15-16.
